
SIGNIFICADO DEL
TEOREMA DE GÖDEL
 | EL VERDADERO SIGNIFICADO DEL TEOREMA DE GÖDEL |
| Elemento | Decidibilidad | |
| Gödel | Sentencia | V o F |
| Church | Expresiones lambda | Equivalencia |
| Turing | Programa | Parada |
| Chaitin | Expresión | Compresión máxima |
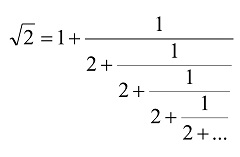
|
( r2 =: (1 + 1.÷(1+r2)) )
(S =: S/I) representa a la expresión fractal (((S/I)/I)I)...
I es el predicado “Soy indemostrable”.
| Una ciencia no puede fundamentarse en sí misma. Necesita un fundamento superior o más profundo. La matemática necesita una metamatemática que la fundamente, pero no formalista, sino conceptual-intuitiva. Este es, en esencia, el verdadero significado del teorema de Gödel. |